Question

A motorboat travels 9 miles downstream (with the current) in 30 minutes. The return trip upstream (against the current) takes 90 minutes.

Answer 1

The speed of the stream is 6 mph, and the speed of the boat is 12 mph.

Explanation:

Downstream:

9 miles in 30 minutes (0.5 hour).

9 mi / 0.5 h = 18 mph

Upstream:

9 miles in 90 minutes (1.5 h).

9 mi / 1.5 h = 6 mph

Let s = speed of stream.

The speed of the stream adds to the speed of the boat downstream and is subtracted fromt he speed of the boat upstream.

Let speed of boat be b.

b + s = 18

b - s = 6

Add the equations.

2b = 24

b = 12

b + s = 18

12 + s = 18

s = 6

The speed of the stream is 6 mph, and the speed of the boat is 12 mph.

Answer 2

Given :

A motorboat travels 9 miles downstream (with the current) in 30 minutes.

The return trip upstream (against the current) takes 90 minutes.

To Find :

The speed of stream and motorboat.

Solution :

Let, speed of stream is u and speed of motorboat is v.

Now, we know distance is same in both case.

Distance( downstream ) = speed × time

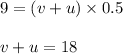`9 = ( v +u ) * 0.5\\\\v + u = 18`....1)

Distance( upstream ) = speed × time

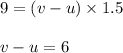`9 = ( v- u ) * 1.5\\\\v-u = 6`....2)

Solving equation 1 and 2 , we get :

v = 12 miles/hour and u = 6 miles/hour

Hence, this is the required solution.