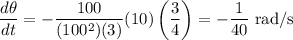Question

A kite 100 ft above the ground moves horizontally at a speed of10 ft/s. At what rate is the angle (inradians) between the string and the horizontal decreasing when 200ft of string have been let out? (Enter your answer as afraction.)

Answer 1

`\displaystyle (d\theta)/(dt)=-(1)/(40)\text{ rad/s}`

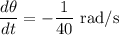
Explanation:

We can model the situation with the diagram below.

The relationship between the angle between the string and the horizontal can be modeled by:

`\displaystyle \tan\theta =(100)/(x)=100x^(-1)`

Differentiate the equation with respect to time t:

`\displaystyle \sec^2(\theta)(d\theta)/(dt)=-100x^(-2)(dx)/(dt)`

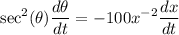
When 200 ft of string have been left out, a = 200.

By the Pythagorean Theorem:

`x=\displaystyle √(200^2-100^2)=√(30000)=100\sqrt3`

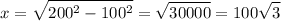
Then it follows that:

`\displaystyle \sec^2\theta =\left((200)/(100√(3))\right)^2=(4)/(3)`

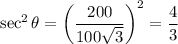
And since the kite moves horizontally at a speed of 10 ft/s, dx/dt = 10.

Substitute:

`\displaystyle \left((4)/(3)\right)(d\theta)/(dt)=-100(100√(3))^(-2)(10)`

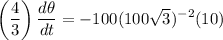
So:

`\displaystyle (d\theta)/(dt)=-(100)/((100^2)(3))(10)\left((3)/(4)\right)=-(1)/(40)\text{ rad/s}`