Question

A man was standing on top of an office building and ‘accidentally' dropped an rock off the roof How tall is the building if the total velocity is 123m/s and the horizontal velocity is 22m/s?

Answer 1

The building is 746.666 meters high.

Step-by-step explanation:

We know the total velocity of the rock (
`v`), in meters per second, and its horizontal speed (
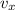`v_(x)`), in meters per second, at the moment right before its impact. It should be noted that the rock is experimenting a parabolic motion, which is the combination of a horizontal motion at constant speed and a free fall, which is an uniform accelerated motion due to gravity.

The final vertical speed of the rock (
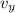`v_(y)`), in meters per second, is determined by the following Pythagoric formula:

`v_(y) = \sqrt{v^(2)-v_(x)^(2)}` (1)

If we know that
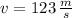`v = 123\,(m)/(s)` and
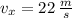`v_(x) = 22\,(m)/(s)`, then the final vertical speed is:

`v_(y) = \sqrt{\left(123\,(m)/(s) \right)^(2)-\left(22\,(m)/(s) \right)^(2)}`

`v_(y) \approx 121.017\,(m)/(s)`

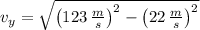
Now we determine the height of the building (
`h`), in meters, by the use of the following kinematic expression:

`h = (v_(y)^(2)-v_(y,o)^(2))/(2\cdot g)` (2)

Where:

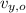`v_(y,o)` - Initial vertical speed of the rock, in meters per second.

`g` - Gravitational acceleration, in meters per square second.

If we know that
`v_(y,o) = 0\,(m)/(s)`,
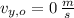`v_(y) \approx 121.017\,(m)/(s)` and
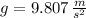`g = 9.807\,(m)/(s^(2))`, then the height of the building is:

`h = (v_(y)^(2)-v_(y,o)^(2))/(2\cdot g)`

`h = (\left(121.017\,(m)/(s) \right)^(2)-\left(0\,(m)/(s) \right)^(2))/(2\cdot \left(9.807\,(m)/(s^(2)) \right))`

`h = 746.666\,m`

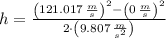
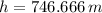
The building is 746.666 meters high.