Answer:
v₃ = - (3 i ^ + 4 j ^) m / s
v₃ = 5 m / s, θ = 233º
Step-by-step explanation:
This is a momentum problem. Let us form a system formed by the three objects so that the forces during the collisions have been internal and the moment is conserved.
Let's start working with the first two objects. As each object moves in a different direction let's work with the components in an xy coordinate system
X axis
initial instant. Before the shock
p₀ₓ = m₁ v₁₀ + 0
final instant. After the crash
p_{fx} = (m1 + m2) vₓ
the moment is preserved
p₀ₓ = p_{fx}
m₁ v₀₁ = (m₁ + m₂) vₓ
vₓ =
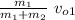
Y axis
initial instant
p_{oy} = 0 + m₂ v₀₂
final moment
p_{fy} = (m₁ + m₂) v_y
the moment is preserved
p_{oy} = p_{fy}
m₂ v₀₂ = (m₁ + m₂) v_y
v_y =
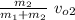
We already have the speed of the set of these two cars, now let's work on this set and vehicle 3
X axis
initial instant
p₀ₓ = (m₁ + m₂) vₓ + m₃ v₃ₓ
final instant
p_{fx} = 0
p₀ₓ = p_{fx}
(m₁ + m₂) vₓ + m₃ v₃ₓ = 0
v₃ₓ =
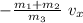
Y Axis
initial instant
p_{oy} = (m₁ + m₂) v_y + m₃ v_{3y}
final moment
p_{fy} = 0
p_{oy} = p_{fy}
(m₁ + m₂) v_y + m₃ v_{3y} = 0
v_{3y} =
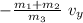
now we substitute the values of the speeds
v₃ₓ =
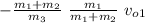
v₃ₓ =
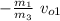
v_{3y} =
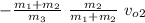
v_{3y} =
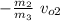
let's calculate
v₃ₓ = - ⅓ 9
v₃ₓ = - 3 m / s
v_{3y} = - ⅔ 6
v_{3y} = - 4 m / s
therefore the speed of vehicle 3 is
v₃ = - (3 i ^ + 4 j ^) m / s
It can also be given in the form of modulus and angles using the Pythagorean theorem
v₃ =

v₃ =
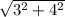
v₃ = 5 m / s
let's use trigonometry for the angle
tan θ' =
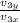
θ' = tan⁻¹ (\frac{v_{3y}}{v_{3x}})
θ' = tan⁻¹ (4/3)
θ' = 53º
That the two speeds are negative so this angle is in the third quadrant, measured from the positive side of the x axis
θ = 180 + θ'
θ = 180 +53
θ = 233º