Question

Find the area of the shaded region

Answer 1

`16\pi - 24√(3)`

Explanation:

The shaded area is the area of the circle minus the area of the hexagon. (It's like a circle with a hexagon cut out of it.)

Area of the circle is
`A_\text{circle} =\pi r^2 = \pi\cdot 4^2 = 16\pi`

Area of the hexagon. The attached image shows two radii drawn that create an equilateral triangle with three 60 degree angles. The blue altitude (marked h) splits that triangle into two 30-60-90 triangles. The bottom side is split into two 2-unit segments. The altitude h is the short leg of the 30-60-90 triangle multiplied by
`√(3)`.

So, the area of one equilateral triangle is
`(1)/(2)(\text{base})(\text{height})=(1)/(2)\cdot 4\cdot 2√(3)=4√(3)`.

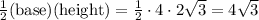The hexagon is made up of 6 such equilateral triangles, so its area is
`A_\text{hexagon}=6\cdot 4√(3)=24√(3)`

Finally, the shaded region has area (circle minus hexagon):

`16\pi - 24√(3)`

Answer 2

Answer: 40

Explanation: