The range of y = - 32x ^ 2 + 90x + 3

Question

asked Aug 21, 2022 63.4k views

1 Answer

Gerky · Answer 1 · 2022-08-25T14:39:09+0000

Given:

The given function is:

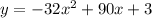
y=-32x^2+90x+3

To find:

The range of the given function.

Solution:

We have,

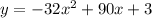
y=-32x^2+90x+3

It is a quadratic function because the highest power of the variable x is 2.

Here, the leading coefficient is -32 which is negative. So, the graph of the given function is a downward parabola.

If a quadratic function is
f(x)=ax^2+bx+c , then the vertex of the quadratic function is:

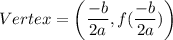
$Vertex=\left((-b)/(2a),f((-b)/(2a))\right)$

In the given function,
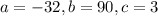a=-32,b=90,c=3 .

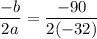
(-b)/(2a)=(-90)/(2(-32))

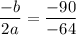
(-b)/(2a)=(-90)/(-64)

(-b)/(2a)=(45)/(32)

The value of the given function at
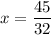x=(45)/(32) is:

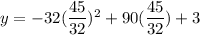
y=-32((45)/(32))^2+90((45)/(32))+3

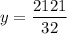
y=(2121)/(32)

The vertex of the given downward parabola is
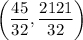$\left((45)/(32),(2121)/(32)\right)$ . It means the maximum value of the function is
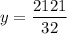y=(2121)/(32) . So,

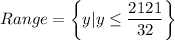
$Range=\left\y\leq (2121)/(32)\right\$

$Range=\left(-\infty, (2121)/(32)\right ]$

Therefore, the range of the given function is
$\left (-\infty, (2121)/(32)\right ]$ .