Answer:
The next three terms of the sequence are 17, 21 and 25.
The 300th term of the sequence is 1197.
Explanation:
The statement describes an arithmetic progression, which is defined by following formula:
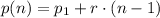 (1)
(1)
Where:
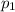 - First element of the sequence.
- First element of the sequence.
 - Progression rate.
- Progression rate.
 - Index of the n-th element of the sequence.
- Index of the n-th element of the sequence.
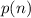 - n-th element of the series.
- n-th element of the series.
If we know that
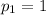 ,
,
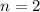 and
and
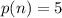 , then the progression rate is:
, then the progression rate is:
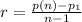

The set of elements of the series are described by
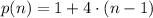 .
.
Lastly, if we know that
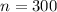 , then the 300th term of the sequence is:
, then the 300th term of the sequence is:
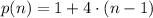
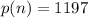
And the next three terms of the sequence are:
n = 5
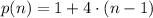
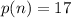
n = 6
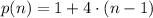
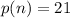
n = 7
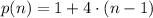
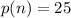
The next three terms of the sequence are 17, 21 and 25.
The 300th term of the sequence is 1197.