Given:
The system of equations are:
(a)
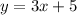

(b)
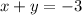

To find:
The intersection points of the given system of equations.
Solution:
(a)
We have,
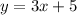 ...(i)
...(i)
 ...(ii)
...(ii)
From (i) and (ii), we get
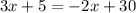
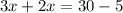
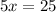

Putting x=5 in (i), we get
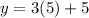
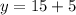
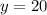
Therefore, the point of intersection is (5,20).
(b)
The given system of equations is:
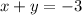

Write these equation in slope intercept form
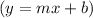 , where m is slope and b is y-intercept.
, where m is slope and b is y-intercept.
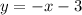 ...(iii)
...(iii)
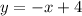 ...(iv)
...(iv)
From the equation (iii) and (iv), it is clear that the slopes of both equations are same, i.e., -1 but the y-intercepts are different, -3 and 4 respectively.
It means the lines are parallel and parallel lines never intersect each other.
Therefore, the point of intersect does not exist because the lines are parallel.