Question

Secants ⎯⎯⎯⎯⎯⎯⎯⎯⎯ and ⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ intersect in the exterior of a circle. ⏜ measures 191° and ⏜ measures 53°. Determine the measure of ∠ EFG.

Answer 1

m(∠EFG) = 69°.

Explanation:

Secants DF and HF intersect each other outside the circle at point F.

By the theorem,

"Measure of angle between intersecting secants is half of the difference of intercepted arcs"

m(∠EFG) =
`(1)/(2)(\text{arc DJH} - \text{arc EG})`

=
`(1)/(2)(191-53)`

=
`(1)/(2)(138)`

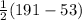
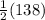
= 69°

Therefore, measure of angle EFG is 69°.