Question

NO LINKS!! Please help me with this problem Part 5gg​

Answer 1

(-2, 0)

Explanation:

Given inequality:

`2x^2+4x < 0`

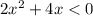
Solve the inequality as though it were an equation:

`\implies 2x^2+4x=0`

`\implies 2x(x+2)=0`

`\implies 2x=0 \implies x=0`

`\implies x+2=0 \implies x=-2`

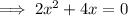
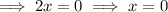
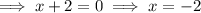
The real solutions to the equation are the boundary points for the solution to the inequality.

Make the boundary points open circles as the original inequality does not include equality.

Three regions have been created:

• x < -2
• -2 < x < 0
• x > 0

Select points from the different regions and test to see if they satisfy the original inequality:

`x=-3 \implies 2(-3)^2+4(-3)=6 > 0`

`x=-1 \implies 2(-1)^2+4(-1)=-2 < 0`

`x=1 \implies 2(1)^2+4(1)=6 > 0`

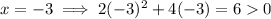
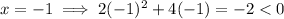
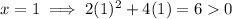
Since x = -3 does not satisfy the original inequality, the region x < -2 is not part of the solution.

Since x = -1 does satisfy the original inequality, the region -2 < x < 0 is part of the solution.

Since x = 1 does not satisfy the original inequality, the region x > 0 is not part of the solution.

Therefore, the solution in interval notation is:

• (-2, 0)

To graph the solution set:

• Place open circles at x = -2 and x = 0.
• Connect the open circles with a line.