Question

Use the concept of the definite integral to find the total area between the graih offo) and theNavis, by taking the limit of the associated right Riemann sum. Write the exact answer. Do not round. (Hint: Extrneeded on those intervals where10) < 0. Remember that the definite integral represents a signed area.)¡(0) = 7,? - 28 on (-2, 2)

Answer 1

Before we start let's remember two important properties of integrals

`\begin{gathered} \int (f(x)\pm g(x))_{}dx=\int f(x)dx\pm\int g(x)dx \\ \\ \int c\cdot f(x)dx=c\cdot\int f(x)dx \end{gathered}`

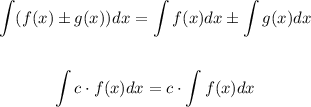
Using that, we can rewrite

`\int ^2_(-2)(7x^2-28)dx`

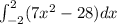
as

`7\int ^2_(-2)x^2dx-28\cdot\int ^2_(-2)dx`

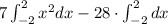
The integral of a monomial is

`\int x^ndx=(x^(n+1))/(n+1),n\\e-1`

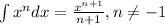
Using it let's integrate the two monomials

`F(x)=\int (7x^2-28)dx=(7x^3)/(3)-28x+C`

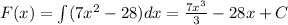
Using that and the Fundamental Theorem of Calculus:

`\int ^b_af(x)dx=F(b)-F(a)`

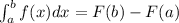
We just gotta evaluate F(x) at 2 and -2.

`\begin{gathered} \int ^2_(-2)(7x^2-28)dx=F(2)-F(-2) \\ \\ \int ^2_(-2)(7x^2-28)dx=((7\cdot2^3)/(3)-28\cdot2)-((7\cdot(-2)^3)/(3)-28\cdot(-2)_{}) \\ \\ \int ^2_(-2)(7x^2-28)dx=-(56)/(3)-56 \\ \\ \int ^2_(-2)(7x^2-28)dx=-56(1+(1)/(3)) \end{gathered}`

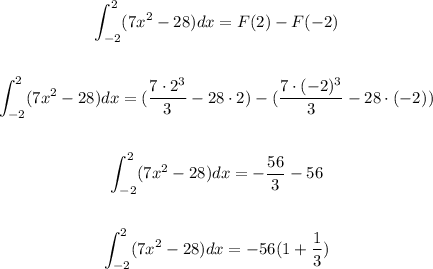
Therefore, the final result is

`\int ^2_(-2)(7x^2-28)dx=-56(1+(1)/(3))`

That's the signed area.