Question

Hi, can you help me with problem D? I’m in high school calculus 1. Thank you!

Answer 1

Applying the next trigonometric identity:

`\sin ^2\alpha+\cos ^2\alpha=1`

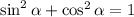
to angle θ, and solving for cos(θ), we get:

`\begin{gathered} \sin ^2\theta+\cos ^2\theta=1 \\ \text{ Substituting with }\sin ^{}\theta=1/3\colon \\ ((1)/(3))^2+\cos ^2\theta=1 \\ (1)/(9)+\cos ^2\theta=1 \\ \cos ^2\theta=1-(1)/(9) \\ \cos ^2\theta=(8)/(9) \\ \cos \theta=\sqrt[]{(8)/(9)} \\ \cos \theta=\frac{\sqrt[]{8}}{3} \\ \cos \theta=\frac{2\sqrt[]{2}}{3} \end{gathered}`

The relation between the cosine and the secant of an angle is:

`\begin{gathered} \sec \varphi=(1)/(\cos\varphi) \\ \text{ Substituting with }\sec \varphi=17/8\colon \\ (17)/(8)=(1)/(\cos\varphi) \\ ((17)/(8))^(-1)=((1)/(\cos\varphi))^(-1) \\ (8)/(17)=\cos \varphi \end{gathered}`

Applying the before mentioned trigonometric identity to angle φ, we get:

`\begin{gathered} \sin ^2\varphi+\cos ^2\varphi=1 \\ \text{ Substituting with cos}\varphi\text{ = 8/17}\colon \\ \sin ^2\varphi+((8)/(17))^2=1 \\ \sin ^2\varphi+(64)/(289)^{}=1 \\ \sin ^2\varphi=1-(64)/(289) \\ \sin ^2\varphi=(225)/(289) \\ \sin \varphi=\sqrt[]{(225)/(289)} \\ \sin \varphi=(15)/(17) \end{gathered}`

Difference formula of cosine

`\cos (\alpha-\beta)=\cos \alpha\cdot\cos \beta+\sin \alpha\cdot\sin \beta`

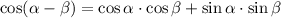
Applying this formula to angles θ and φ, and substituting with the values found, we get:

`\begin{gathered} \cos (\theta-\varphi)=\cos \theta\cdot\cos \varphi+\sin \theta\cdot\sin \varphi \\ \cos (\theta-\varphi)=\frac{2\sqrt[]{2}}{3}\cdot(8)/(17)+(1)/(3)\cdot(15)/(17) \\ \cos (\theta-\varphi)=\frac{16\sqrt[]{2}}{51}+(15)/(51) \\ \cos (\theta-\varphi)=\frac{16\sqrt[]{2}+15}{51} \end{gathered}`