Given:
A function
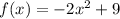
and value of g(x) at x.
To find:
Maximum value of both functions.
Step-by-step explanation:
For criticle points find f'(x) = 0 and f''(x)>0. Then value will be maximum.
Solution:
Now, first derivative is
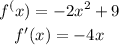
Now, put f'(x)=0 and criticle point will be 0.
Now,
![f^{^^(\prime)^(\prime)}(x)=-4]()
As second derivative of function is negetive at x=0. So, we will get maximum at x=0
So, At x=0
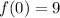
So, maximum value of f(x) is 9 and maximum value of g(x) is 11.
Hence, this is the maximum values of f(x) and g(x).