Question

Find the approximate mean and standard deviation of the following data.

Answer 1

Given the data in the table, to find the approximate mean we would need to find the midpoints for the given intervals.

The midpoint was gotten from the average of the upper and lower class intervals.

We can then find the approximate mean using the formula below.

`\bar{x}(Mean)=\frac{\sum^{}_{}fx}{\sum^{}_{}f}`

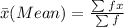
Therefore,

`\begin{gathered} \bar{x}=((8*3.5)+(11.5*3)+(19.5*9)+(27.5*5))/(8+3+9+5) \\ \bar{x}=(28+34.5+175.5+137.5)/(25) \\ \bar{x}=(375.5)/(25) \\ \bar{x}=15.02 \end{gathered}`

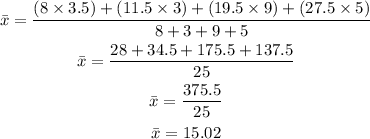
To find the standard deviation we would use the formula below;

`\begin{gathered} \sigma^2=\frac{\sum^{}_{}f(x-\bar{x})^2}{\sum^{}_{}f} \\ ^{} \end{gathered}`

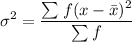
Thus;

`\begin{gathered} \sigma^2=(8(3.5-15.02)^2+3(11.5-15.02)^2+9(19.5-15.02)^2+5(27.5-15.02)^2)/(25) \\ =(1061.6832+37.1712+180.6336+778.752)/(25) \\ \sigma^2=82.3296 \\ \sigma=\sqrt[]{82.3296} \\ \sigma=9.074 \end{gathered}`

Answer:

Therefore, the approximate mean and standard deviation is 15.02 and 9.074 respectively