We can find the reason if we simply follow the steps to find the inverse of a function.
Let us find the inverse of:
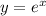
Swap x and y in the function:
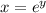
Solve for y. This can be done by finding the logarithm of both sides:
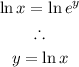
This is one proof.
Another proof can be to compare the graphs of both expressions. If two functions are inverses of one another, the graphs are symmetrical because of the domain and range swap between them. The graph is shown below: