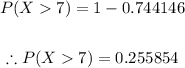The probability that an adult knows what he will have for dinner: p = 0.28
We define event A as follows:
A: An adult knows what he will have for dinner
Then, if we ask 22 adults, the probability that more than 7 will say "yes" is given by the binomial distribution:
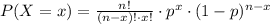
From the problem, we identify:
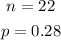
Then:
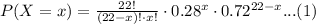
Using the definition of the complement of an event, the probability that more than 7 will say yes is equivalent to:
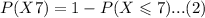
Where:
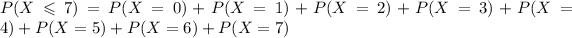
Using (1), we find each probability:
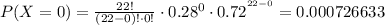
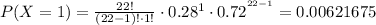
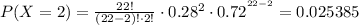
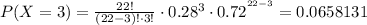

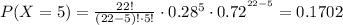
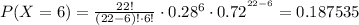
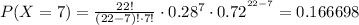
Taking the sum of all of them, and using (2):