Question

Find the measure of all the angles and all the arcs in the figure below.Please

Answer 1

• mAD=60°

,

• mBF=60°

,

• mCF=60°

,

• m∠COD=120°

,

• m∠B=90°

,

• m∠C=30°

,

• m∠D=60°

,

• m∠DAB=120°

Step-by-step explanation:

The line AC is the diameter of the circle.

`\begin{gathered} m\widehat{AC}=180\degree \\ m\widehat{AC}=m\widehat{AD}+m\widehat{DC} \\ 180\degree=m\widehat{AD}+120\degree \\ m\widehat{AD}=180\degree-120\degree \\ m\widehat{AD}=60\degree \end{gathered}`

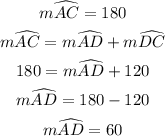
Similarly, line DF is a diameter, thus:

`\begin{gathered} m\widehat{DF}=180\degree \\ m\widehat{DF}=m\widehat{AD}+m\widehat{AB}+m\widehat{BF} \\ 180\degree=60\degree+60\degree+m\widehat{BF} \\ m\widehat{BF}=180\degree-120\degree \\ m\widehat{BF}=60\degree \end{gathered}`

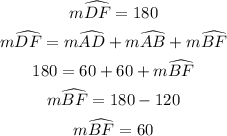
In like manner, using line DF:

`\begin{gathered} m\widehat{DF}=180\degree \\ m\widehat{DF}=m\widehat{DC}+m\widehat{CF} \\ 180\degree=120\degree+m\widehat{CF} \\ m\widehat{CF}=180\degree-120\degree \\ m\widehat{CF}=60\degree \end{gathered}`

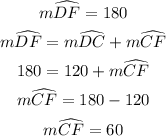
Angle COD is the central angle subtended by arc CD at the centre.

`\begin{gathered} m\angle\text{COD}=m\widehat{CD} \\ m\angle\text{COD}=120\degree \end{gathered}`

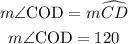
Angle B is the angle subtended by the diameter AC at the circumference of the circle. The angle in a semicircle is 90 degrees, therefore:

`m\angle B=90\degree`

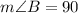
Angle C is the angle subtended by arc AB at the circumference.

`\begin{gathered} m\widehat{AB}=2* m\angle C \\ 60\degree=2* m\angle C \\ m\angle C=(60\degree)/(2) \\ m\angle C=30\degree \end{gathered}`

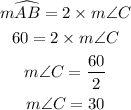
Next, we find the measure of angle D.

In Triangle AOD,

`\begin{gathered} m\angle O=\text{mAD}=60\degree \\ OD=OA(\text{radi}i) \\ \triangle\text{AOD is Isosceles} \\ \implies\angle O+2\angle D=180\degree \\ 60\degree+2m\angle D=180\degree \\ 2m\angle D=120\degree \\ m\angle D=60\degree \end{gathered}`

Finally, we find the measure of angle DAB.

`\begin{gathered} m\angle\text{DAB}=m\angle\text{DAO}+m\angle\text{CAB} \\ =60\degree+60\degree \\ =120\degree \end{gathered}`