Question

A bucket begins weighing 20 pounds, including the sand it holds. The bucket is to be lifted to the top of a 25 foot tall building by a rope of negligible weight. However, the bucket has a hole in it, and leaks 0.1 pounds of sand each foot it is lifted. Find the work done lifting the bucket to the top of the building

Answer 1

`\begin{equation*} 468.75\text{ foot-pound} \end{equation*}`

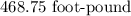
Step-by-step explanation

Let the bucket be lifted x feet.

The weight of the bucket at x feet is given by:

`20-0.1x`

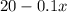
The work done in lifting the bucket by dx feet is:

`dW=(20-0.1x)dx`

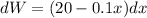
The total work done is the integral of the work done in lifting the bucket x feet, that is:

`W=\int(20-0.1x)dx`

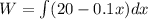
Hence, the work done in lifting the bucket 25feet is:

`\begin{gathered} W=\int_0^(25)(20-0.1x)dx \\ \\ W=(20x-(0.1x^2)/(2))_0^(25) \\ \\ W=(20*25-(0.1*25^2)/(2))-(20*0-(0.1*0^2)/(2)) \\ \\ W=500-31.25 \\ \\ W=468.75\text{ foot-pound} \end{gathered}`

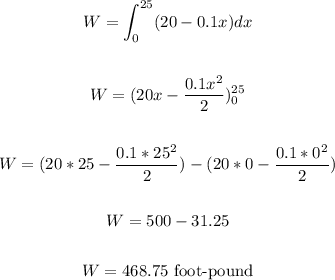
That is the answer.