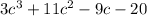We need to make the product of a binomial times a trinomial of the form:
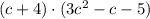
So we use distributive roerty, making sure that we multiply each term of the first binomial times each term of the trinomial.
We start by multiplying c times each of the three terms in the trinomial expression, and after that we do the product of "4" times each of the three terms of the trinomial:
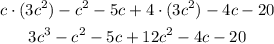
and to follow this, we combine the like terms that we have produced in the product. These are the terms in c-squared, and the terms in c: