Answer:
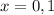
Step-by-step explanation:
We were given that:
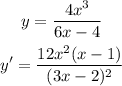
b)
The horizontal tangent line refers to where a function's derivative is zero since horizontal lines have a slope of zero.
When the function has horizontal tangent lines, we have:
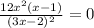
Let's proceed to solve, we have:
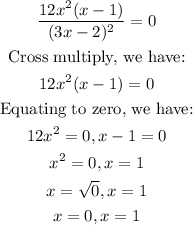
Therefore, x is equal to: 0, 1