Question

A scientist begins with 100 milligrams of a radioactive substance, which decays exponentially.after 9 hours 55mg of the substance remains How many milligrams will remain after 21 hours? Round the answer to the nearest whole number and include units

Answer 1

We have that the general expression for a function with exponential growth or decay is:

`f(t)=ab^t`

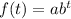
where 'a' represents the initial value, 'b' represents the growth or decay and t represents the time.

In this case, we have that a = 100, since that is the initial population (100 mg of radioactive substance). Also, since we have that after 9 hours, 55 mg of the substance remains, we have the following equation:

`f(9)=55`

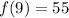
now, given the exponential function, with a = 100, we have:

`f(t)=100b^t`

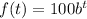
then, combining both expressions, we get:

`f(9)=100b^9=55`

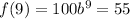
solving for b, we have:

`\begin{gathered} 100b^9=55 \\ \Rightarrow b^9=(55)/(100) \\ \Rightarrow b=\sqrt[9]{(55)/(100)}=0.935 \\ b=.935 \end{gathered}`

then, the function is defined as follows:

`f(t)=100\cdot(0.935)^t`

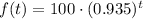
finally, to find out how many milligrams will remain after 21 hours, we can make t = 21 and evaluate the function:

`\begin{gathered} t=21 \\ \Rightarrow f(21)=100(0.935)^(21)=24.38 \\ f(21)=24.38mg \end{gathered}`

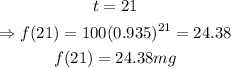
therefore, there will be 24.38mg after 21 hours