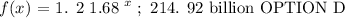SOLUTION:
Step 1:
In this question, we are given the following:
A scientist has discovered a new strain of bacteria.
The bacteria grows exponentially at a rate of 68% each hour as shown in the table below.
Identify the equation used to calculate the growth, and estimate the population of the bacteria when the time has reached 10 hours.
Step 2:
The details of the solution are as follows:
Since the bacteria grows exponentially at a rate of 68% each hour, and the initial population is 1. 2 billiion.
This means that:
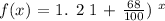

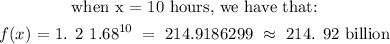
CONCLUSION:
The final answer is: