Question

it says the area of a rectangular ballroom is 800m2 and the perimeter is 120m.what are the dimension of the ballroom

Answer 1

20m and 40m

Step-by-step explanation

A rectangular ballroom has two dimensions: length and width,

The perimeter is the sum of all the sides of the rectangle,

`P=L+L+W+W=2L+2W`

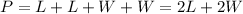
The area is the product of these two dimensions,

`A=L\cdot W`

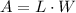
We know that the perimeter is 120m and the area is 800m². Replacing in the equations above, we have two equations with two variables L and W,

`\begin{gathered} 120=2L+2W \\ 800=LW \end{gathered}`

Solve the first equation for W. Subtract 2L from both sides,

`\begin{gathered} 120-2L=2L-2L+2W \\ 120-2L=2W \end{gathered}`

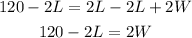
And divide both sides by 2,

`\begin{gathered} (120-2L)/(2)=(2W)/(2) \\ 60-L=W \end{gathered}`

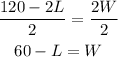
The next step is to replace W by this expression in the second equation,

`800=L(60-L)`

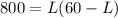
Now we have to solve this equation for L. Apply the distributive property on the right side of the equation,

`800=60L-L^2`

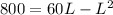
Subtract 800 from both sides,

`\begin{gathered} 800-800=-L^2+60L-800 \\ 0=-L^2+60L-800 \end{gathered}`

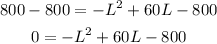
We have a quadratic equation to find the zeros of the polynomial. To solve it, we can use the quadratic formula,

`\begin{gathered} ax^2+bx+c=0 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}`

In this case x = L, a = -1, b = 60 and c = -800,

`L=\frac{-60\pm\sqrt[]{60^2-4\cdot(-1)\cdot(-800)}}{2\cdot(-1)}`
`L=\frac{-60\pm\sqrt[]{3600-3200}}{-2}=\frac{-60\pm\sqrt[]{400}}{-2}=(-60\pm20)/(-2)`

We have two possible results for L,

`L_1=(-60+20)/(-2)=20`
`L_2=(-60-20)/(-2)=40`

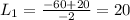
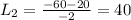
To find the width of the ballroom we have to replace L into the equation we found when we solved the first equation for W,

`W=60-L`

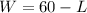
So we have two possible results for W as well,

`W_1=60-L_1=60-20=40`
`W_2=60-L_2=60-40=20`

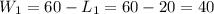
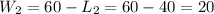
Note that the pairs are 20m and 40m or 40m and 20m. Hence, we can say that the dimensions of the ballroom are 20m and 40m