Question

Find the area of triangle ABC then find the area of triangle XYZ

Answer 1

Given:

The objective is to find the area of triangle ABC and XYZ.

Step-by-step explanation:

The general formula to find the area of a triangle is,

`A=(1)/(2)* b* h\text{ . . . . .(1)}`

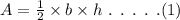
To find the area of triangle ABC:

The height of the triangle DC can be calculated using the Pythagorean theorem of triangle ADC.

`DC=\sqrt[]{AC^2-AD^2}\ldots.\text{ .(2)}`

On plugging the given values in equation (2),

`\begin{gathered} D\C=\sqrt[]{13^3-5^2} \\ =\sqrt[]{169-25} \\ =\sqrt[]{144} \\ =12 \end{gathered}`

Thus, the height of triangle ABC is 12.

Since it is given in the figure that AD = DB = 5.

So the base of the triangle AB = 5 + 5 = 10.

Now, substitute the obtained values in equation (1).

`\begin{gathered} A(\text{ABC)}=(1)/(2)* AB* DC \\ =(1)/(2)*10*12 \\ =60 \end{gathered}`

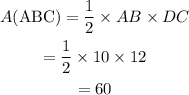
To find the area of triangle XYZ:

Since it is given in the figure that XW= WY = 15.

So the base of the triangle XY = 15 + 15 = 30.

The height of the triangle is WZ = 36.

Now, substitute the obtained values in equation (1).

`\begin{gathered} A(XYZ)=(1)/(2)* XY* WZ \\ =(1)/(2)*30*36 \\ =540 \end{gathered}`

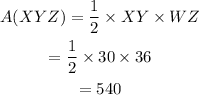
Hence, the area of triangle ABC is 60 square units and the area of triangle XYZ is 540 square units.