Given:
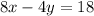
To complete the table, let's substitute the values that are known and find the unknown.
a) y = 0
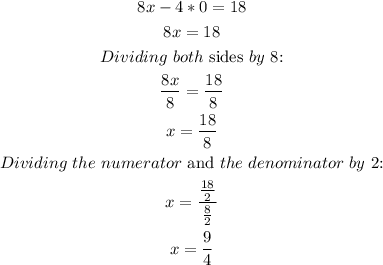
The first point is (9/4, 0).
b) x = 0

The first point is (0, -9/2).
c) x = 1

The third point is (1, -5/2).
d) y = 3

The fourth point is (15/4, 3).
Answer:
x 9/4 0 1 15/4
y 0 -9/2 -5/2 3