Answer:
-8/15
Explanations:
Given the following parameters
tan(x) = 4
sin(x) is positive
Required
tan(2x)
According to the double angle formula
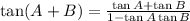
Applying this formula to expand tan(2x)
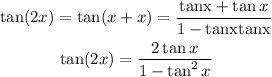
Substitute tan(x) = 4 into the expression:
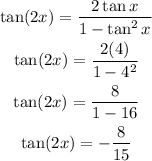
Hence the value of tan(2x) is given as -8/15