Question

Finding solutions in an interval for a trigonometric equation with a squared function

Answer 1

Given the equation:

`\cos ^2x-4\cos x+3=0`

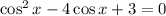
Let's find all the solutions of the equation in the interval: [0, 2π).

To find the solution, take the following steps.

Step 1:

Let u = cos x.

Then factor the left side of the equation.

`\begin{gathered} u^2-4u+3=0 \\ \\ (u-3)(u-1)=0 \end{gathered}`

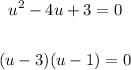
Step 2:

Now, replace u with cosx:

`(\cos x-3)(\cos x-1)=0`

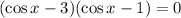
Step 3.

Equate the individual factors to zero and solve for x:

`\begin{gathered} \cos x-3=0 \\ \cos x=3 \\ \\ \text{The range of cosine is }-1\le y\le1.\text{ Hence }3\text{ does not fall in the range.} \end{gathered}`
`\begin{gathered} \cos x-1=0 \\ \cos x=1 \\ \text{Take the cos inverse of both sides:} \\ x=\cos ^(-1)(1) \\ x=0 \end{gathered}`

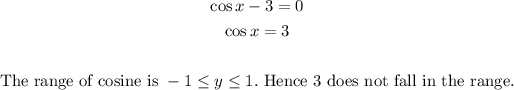
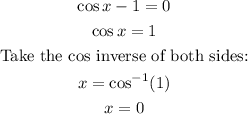
This cosine function is positive in the first and fourth quadrants.

To find the second solution, subtract the reference angle from 2π to get the second solution in quadrant IV.

`\begin{gathered} x=2\pi-0 \\ \\ x=2\pi \end{gathered}`

Therefore, the solution in the given interval is:

x = 0

ANSWER:

x = 0