Question

A 20 m telephone cable (m=100 kg) is strung between two poles with a tension of 2000 N. the wind creates a standing wave across the table with a wavelength of 0.5 M. What is the frequency of the wave on the cable? hint this problem requires using two equations! A) 40 HzB) 20 HzC) 4.5 HzD) 400 Hz

Answer 1

By solving the wave equation for a string, we can find out that the velocity of a wave on it is:

`v=\sqrt[\placeholder{⬚}]{(T)/((m)/(L))}`

Where T is the tension, m is the mass and L is the length. We can calculate in our case, which leaves us with:

`v=\sqrt[\placeholder{⬚}]{(2000)/((100)/(20))}=20(m)/(s)`

So the velocity in which a wave propagates on this cable is 20 m/s. We can also calculate its fundamental vibration frequency, which is:

`f_1=(v)/(2L)=(20)/(2*20)=0.5Hz`

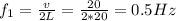
However, this is when there is a single "half-wave" on the cable. As we know from the exercise, the wavelength (i.e. the full wave) is 0.5m, so our cable can fit 20/0.5 or 40 full waves, which is 80 half waves.

With this in mind, we can use the formulas for a standing wave:

`f=n.f_1=80*0.5=40Hz`

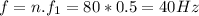
Then, our final answer is f=40Hz