The sum of the speeds of two trains is 722.4 miles per hour. If the speed of the first train is 9.6mph faster than that of the second train, find the speeds of each .

Question

asked Jan 14, 2023 53.1k views

1 Answer

Mansa · Answer 1 · 2023-01-19T21:02:43+0000

If the speed of the second train is represented by x, then the first train's speed is: x + 9.6

Then, we can form the following equation:

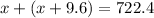
Next, solve for x:

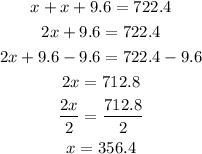
$\begin{gathered} x+x+9.6=722.4 \\ 2x+9.6=722.4 \\ 2x+9.6-9.6=722.4-9.6 \\ 2x=712.8 \\ (2x)/(2)=(712.8)/(2) \\ x=356.4 \end{gathered}$

This is the speed of the second train, and

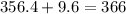
This is the speed of the first train

Answer:

the speed of the first train: 366 mph

the speed of the second train: 356.4 mph