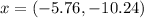Question

Solve the quadratic equation by completing the square.x ^ 2 + 16x + 59 = 0First, choose the appropriate form and fill in the blanks with the correct numbers. Then, solve the equation. Round your answer to the nearest hundredth. If there is more than one solution, separate them with commas.

Answer 1

Given:

There are given the quadratic equation:

`x^2+16x+59=0`

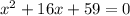
Step-by-step explanation:

To find the value of x by using completing the square, first, we need to subtract 59 on both sides of the given equation:

So,

From the given equation:

`\begin{gathered} x^2+16x+59=0 \\ x^2+16x+59-59=0-59 \\ x^2+16x=-59 \end{gathered}`

Now,

Take half of the x term and square it:

So,

From the x term,

`\lbrack16\cdot(1)/(2)\rbrack^2=64`

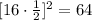
Then,

Add 64 on both sides of the above equation.

So,

`\begin{gathered} x^2+16x=-59 \\ x^2+16x+64=-59+64 \\ x^2+16x+64=5 \\ (x+8)^2=5 \end{gathered}`

Hence, an option first is correct:

`(x+8)^2=5`

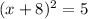
Now,

From the above square:

`\begin{gathered} (x+8)^2=5 \\ x+8=\pm\sqrt[]{5} \end{gathered}`

Then,

Subtract 8 from both sides of the equation;;

So,

`\begin{gathered} x+8=\pm\sqrt[]{5} \\ x+8-8=\pm\sqrt[]{5}-8 \\ x=\pm\sqrt[]{5}-8 \\ x=\sqrt[]{5}-8,\pm\sqrt[]{5}-8 \\ x=-5.7639,-10.236067 \end{gathered}`

Final answer:

Hence, the value of x is shown below:

`x=(-5.76,-10.24)`