![\begin{gathered} f(x)\text{ =}(2x-1)/(50-x) \\ To\det er\min e\text{ the horizontal asymptote, w}e\text{ compare the degre}e\text{ of x in the numerator and denominator} \\ \end{gathered}]()
The degree of x in the numerator is 1 and the degree of x in the denominator is 1 as well
There we go ahead to divide the coefficient of x in the numerator by that in the denominator
The coefficient of x in the numerator is 2 and the coefficient of x in the denominator is -1
Therefore
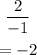
The horizontal asymptote is -2