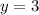Question

Find the horizontal asymptote.y =3x - 1x + 3y = [?]

Answer 1

We have the next function

`y=(3x-1)/(x+3)`

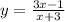
And we must find the horizontal asymptote.

In order to find the horizontal asymptote we must divide all the rational function by the variable with the greater exponent and then we must find the limit when x -> ∞

In this case, the variable with the greater exponent is x, so we must divde the rational function by x

`((3x-1)/(x))/((x+3)/(x))=((3x)/(x)-(1)/(x))/((x)/(x)+(3)/(x))`

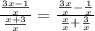
Then, we must find the limit when x -> ∞

`\begin{gathered} \lim _(x\to\infty)((3x)/(x)-(1)/(x))/((x)/(x)+(3)/(x)) \\ \text{ Simplifying} \\ \lim _(x\to\infty)(3-(1)/(x))/(1+(3)/(x)) \\ \end{gathered}`

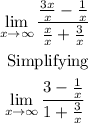
Finally, the limit is

`(3-(1)/(\infty))/(1+(3)/(\infty))`

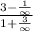
Using that when we divide a number by infinity the answer is 0

`=(3-0)/(1+0)=(3)/(1)=3`

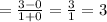
So, the horizontal asymptote is

`y=3`

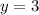
ANSWER:

`y=3`