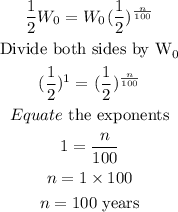Answer
Step-by-step explanation
The weight (W kg) of a decaying radio active substance after n years is given by:
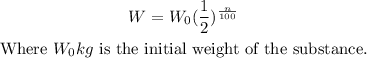
To find the number of years for the radioactive substance to decay to half of its initial weight, it implies the weight of the substance at that number of years will be:
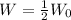
Therefore,