Question

How many and of which kind of roots does the equation f(x)= 2x^4-9x^3+17x^2-16x+6 have?

Answer 1

Given that,

`f\mleft(x\mright)=2x^4-9x^3+17x^2-16x+6`

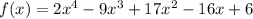
To find number of roots

we know that,

Roots of equations can be defined as “the value of x that makes f(x) = 0” or can be called as the zeros of the equation.

The number of zeros of a polynomial depends on the degree of the equation y = f(x). All such domain values of the function, for which the range is equal to zero, are called the zeros of the polynomial.

Also, we know that for the nth degree polynomial, the number of zeros corresponding to the polynomial is equal to n.

Here,

The degree of polynomial is 4.

Hence there are 4 roots and all the roots are real.

Answer is: f(x) has 4 real roots.