Question

A private jet can fly 2016 miles in three hours with a tailwind, but only 1884 miles in three hours with a headwind. What is the speed of the jet in still air? What is the speed of the wind?

Answer 1

The tailwind means the jet is flying with the wind while, the headwind means the jet is flying against the wind

We first the speed for eac case

For the Tailwind Speed (TS)

`\begin{gathered} TS=\frac{2016\text{miles}}{3\text{hours}} \\ TS=672mihr^(-1) \end{gathered}`

The speed of the Tailwind is 672 miles per hour

For the Headwind Speed (HS)

`\begin{gathered} HS=\frac{1884\text{miles}}{3\text{hours}} \\ HS=628mihr^(-1) \end{gathered}`

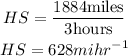
The speed of the Headwind is 628miles per hour

Now, We will now find the speed of the jet in still air as well as the speed of the wind

Let u denotes the speed of the jet in still air, and let v denotes the speed of the wind

This therefore implies that (Note: The tailwind means the jet is flying with the wind)

`u+v=672`

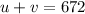
and (Note: the headwind means the jet is flying against the wind)

`u-v=628`

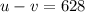
We will solve the two equation simultaneously

`\begin{gathered} u+v=672\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots(1) \\ u-v=628\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\text{.}(2) \\ \end{gathered}`

Equation (1) + equation (2)

`\begin{gathered} (u+u)+(v-v)=672+628 \\ 2u+0=1300 \\ 2u=1300 \\ u=650 \end{gathered}`

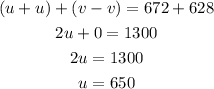
Substitute the value of u into equation (1)

`\begin{gathered} u+v=672 \\ 650+v=672 \\ v=672-650 \\ v=22 \end{gathered}`

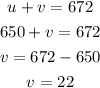
Therefore,

The speed of the jet in still air is 650 mi/hr

The speed of the wind is 22 mi/hr