We are given the following two functions
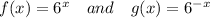
To find the point of intersection we have to equate the functions
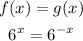
Let us solve the equation for x
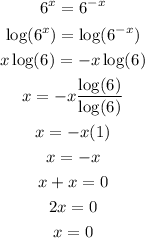
Now substitute this value of x into the function f(x) or g(x) (you will get the same value)
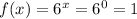
Therefore, the point of intersection is (0, 1)
This is the point where the two functions intersect each other.
As you can see, the two functions intersect at the point (0, 1)