To find the central angle of a polygon we just divide 360° by the number of sides that the polygon has, in this case, we have a pentagon, then the central angle of the polygon is:
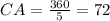
In the figure this angle is represented like this:
If we bisect this angle, which is dividing it by 2, we get the angle θ:
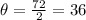
We know that the cosine of the angle θ is:
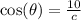
By solving for c from this ratio we get:
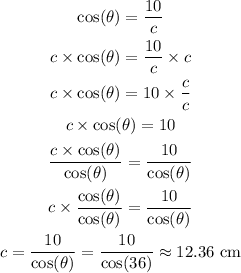
Then, the measure of the radius equals 12.36 cm