Question

Consider the first six terms in the sequence -11,-4,3,10,17,24Which statements are correct?A. The 10th term in this sequence is 52B. The 15th term in this sequence is 123C. The 30th term in this sequence is 192D. The recursive formula is E. The explicit formula is

Answer 1

Notice that the given sequence has a common difference of 7. Then, the sequence is an arithmetic sequence with first term -11 and common difference of 7.

The recursive formula for a sequence with those characteristics, is:

`\begin{gathered} a_n=a_(n-1)+7 \\ a_1=-11 \end{gathered}`

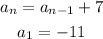
The explicit formula for a sequence with those characteristics, is:

`\begin{gathered} a_n=-11+7(n-1) \\ =-11+7n-7 \\ =7n-18 \end{gathered}`

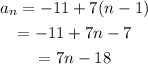
Use the explicit formula to find the 10th term, the 15th term and the 30th term:

`\begin{gathered} a_(10)=-11+7(10-1) \\ =-11+7\cdot9 \\ =-11+63 \\ =52 \end{gathered}`
`\begin{gathered} a_(15)=-11+7(15-1) \\ =-11+7\cdot14 \\ =-11+98 \\ =87 \end{gathered}`
`\begin{gathered} a_(30)=-11+7(30-1) \\ =-11+7\cdot29 \\ =-11+203 \\ =192 \end{gathered}`

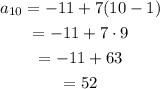
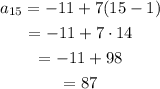
Check each statement to see if they are correct or not:

A: True

B: False

C: True

D: False

E: True