Given:
The Jones family took a 20-mile canoe ride down the Indian River [with the current] in 4 hours and The next day, the return trip back up the river [against the current] took 10 hours.
To find:
the rate of the canoe in still water and the rate of the current.
Solution:
Let x be the rate canoe in still water and y be the rate of current.
So, the rate of canoe with the current will be (x + y). So, by the given condition
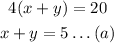
The rate of canoe against the current will be (x - y). So, by the given condition:
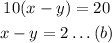
Add (a) and (b), to get:

Substitute x = 3.5 in (a),
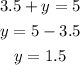
Thus, the rate of canoe in still water is 3.5 mph and the rate of current is 1.5 mph.