Given:
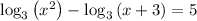
We have:
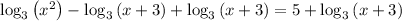
Simplify:
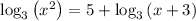
Apply the properties of logarithms:
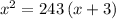
Simplify:

We solve using the general formula for quadratic equations, where:
a = 1
b = - 243
c = - 729
So:

Separate the solutions:
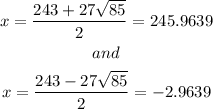
Therefore, the largest value of x is 245.9639
Answer: x = 245.9639