Question

Solve a system of equations above using elimination write your answer in the form (x,y)2x-y=34x-2y=10

Answer 1

To solve the system of equations:

`\begin{gathered} 2x-y=3 \\ 4x-2y=10 \end{gathered}`

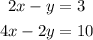
by elimination we need to add the equations to eliminate one of the variables, to do this we need the one of the variables to have the same coefficient. If we multiply the first equation by minus two we have the following system:

`\begin{gathered} -4x+2y=-6 \\ 4x-2y=10 \end{gathered}`

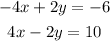
Now we add the equations, then we have:

`\begin{gathered} (-4x+2y)+(4x-2y)=-6+10 \\ 0=4 \end{gathered}`

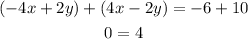
But this is clearly a contradiction (since 0 is not equal to 4). Therefore we conclude that the system of equations does not have a solution.