Question

A customer at a specialty coffee shop observed the amount of time, in minutes, that each of 20 customers spent waiting to receive an order. The results are recorded in the table below.Time (min) to Receive Order3.34.13.92.54.75.24.53.53.66.33.54.94.65.02.83.62.13.95.32.8Find the mean and sample standard deviation of these data. Round to the nearest hundredth.mean _______sample standard deviation ________

Answer 1

Mean:

Standard deviation:

`s=\sqrt[]{\frac{\Sigma(x_i-\bar{x})^2}{n-1}}`

Step by step:

1. Deviation: Subtract the mean from each data:

`\begin{gathered} (x_i-\bar{x}) \\ \\ 3.3-4.005=-0.705 \\ 4.1-4.005=0.095 \\ 3.9-4.005=-0.105 \\ 2.5-4.005=-1.505 \\ 4.7-4.005=0.695 \\ 5.2-4.005=1.195 \\ 4.5-4.005=0.495 \\ 3.5-4.005=-0.505 \\ 3.6-4.005=-0.405 \\ 6.3-4.005=2.295 \\ 3.5-4.005=-0.505 \\ 4.9-4.005=0.895 \\ 4.6-4.005=0.595 \\ 5.0-4.005=0.995 \\ 2.8-4.005=-1.205 \\ 3.6-4.005=-0.405 \\ 2.1-4.005=-1.905 \\ 3.9-4.005=-0.105 \\ 5.3-4.005=1.295 \\ 2.8-4.005=-1.205 \end{gathered}`

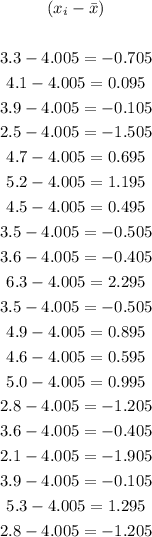
2. Square each deviation:

`\begin{gathered} (x_i-\bar{x})^2 \\ \\ (-0.705)^2=0.497025 \\ (0.095)^2=9.025*10^(-3) \\ (-0.105)^2=0.011025 \\ (-1.505)^2=2.265025 \\ (0.695)^2=0.483025 \\ (1.195)^2=1.428025 \\ (0.495)^2=0.245025 \\ (-0.505)^2=0.255025 \\ (-0.405)^2=0.164025 \\ (2.295)^2=5.267025 \\ (-0.505)^2=0.255025 \\ (0.895)^2=0.801025 \\ (0.595)^2=0.354025 \\ (0.995)^2=0.990025 \\ (-1.205)^2=1.452025 \\ (-0.405)^2=0.164025 \\ (-1.905)^2=3.629025 \\ (-0.105)^2=0.011025 \\ (1.295)^2=1.677025 \\ (-1.205)^2=1.452025 \end{gathered}`

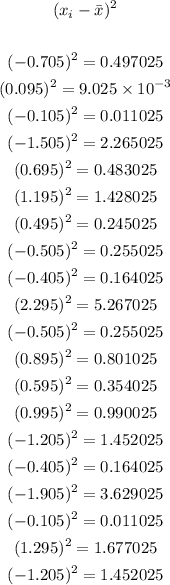
3. Add the square deviations:

`\Sigma(x_i-\bar{x})^2=21.4095`

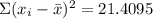
4. Divide the sum by one less than the number of data and take the square root of it to finally get the standard deviation:

`s=\sqrt[]{\frac{\Sigma(x_i-\bar{x})^2}{n-1}}=\sqrt{(21.4095)/(20-1)}=\sqrt{(21.4095)/(19)}=1.06`