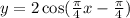Question

(coWrite a cosine function that has an amplitude of 2, a midline of 5 and a period of 8.

Answer 1

Given

A cosine function has an amplitude of 2, a midline of 5 and a period of 8.

To find:

A cosine function.

Step-by-step explanation:

Let the function be,

`y=A\cos(wx+\varphi)`

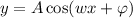
Since amplitude is 2.

Then,

`A=2`

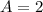
Also, since the period is 8.

Then,

`\begin{gathered} w=(2\pi)/(8) \\ =(\pi)/(4) \end{gathered}`

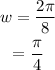
And, since midline is 5.

Then,

`\begin{gathered} \pi=(\pi)/(4)x+\varphi \\ \varphi=\pi-(\pi)/(4)x \\ Since\text{ }midline\text{ }is\text{ }5. \\ Then,\text{ }x=5 \\ \Rightarrow\varphi=\pi-(5\pi)/(4) \\ \Rightarrow\varphi=(4\pi-5\pi)/(4) \\ \Rightarrow\varphi=-(\pi)/(4) \end{gathered}`

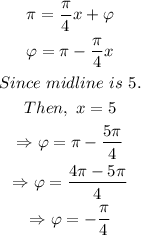
Hence, the cosine function is,

`y=2\cos((\pi)/(4)x-(\pi)/(4))`