The given function is:

It is required to factor the expression for the function in order to find the zero.
To do this, write the function in factored form and then equate it to zero, finding the values of x.
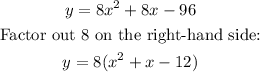
Rewrite the expression in parentheses:
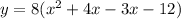
Note that this was done by making sure that the product of the coefficients of x in the expression is equal to the constant term -12.
Next, factorize the expression in parentheses:
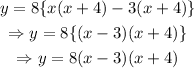
Substitute y=0 into the function to find the zeros:
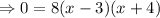
Divide both sides by 8:
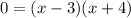
The product of two numbers is zero implies that either of them must be zero:
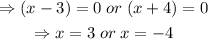
Hence, the correct answer is option B.