Dividing the second equation by 5 we get:

Substituting the last equation in the first one we get:
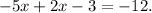
Adding like terms we get:
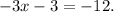
Adding 3 to the above equation we get:
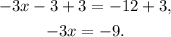
Dividing the above equation by -3 we get:
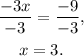
Finally, substituting x=3 in y=2x-3 we get:
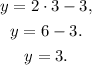
Answer: One solution (3,3).