Question

A sculptor is planning to order a rectangular of composite stone to sculpt a lion. The sculptor anticipated that the lion will be 5 feet long, about 2 feet wide and at the tallest part of the lions body, have a height of 3.5 feet. The composite stone weighs 40 pounds per cubic foot. To the nearest cubic foot, estimate the weight of the smallest rectangular block that the sculptor must purchase in order to create his statue

Answer 1

In order to sculpt the lion, the scupltor must have, at least, a rectangular composite that has the maximum dimensions of the final sculpture.

Thereby,

`5ft\cdot2ft\cdot3.5ft=35ft^3`

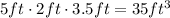
The rectangular composite would need to have a volume of 35 cubic feet.

Now, let's use a rule of three to calculate the weight of the composite, since we're given its density:

This way,

`x=(35\cdot40)/(1)\rightarrow1400lbs`

We can conclude that the weight of the smallest rectangular block that the sculptor must purchase in order to create his statue is 1400 lbs