Using the data from the question, we draw the following triangles:
The dimensions are in feet.
Now, the two triangles are proportional, so if we compute the ratio between the height and the basis of the first triangle, and then we do the same with the second, we must obtain the same number:
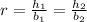
Replacing the dimensions of the triangles in the last equation, we get:
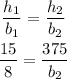
From the last equation we can compute b2, the basis of the second triangle, doing that we find that:
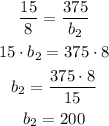
So the second triangle's base is:
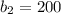
(in feet)
Answer
A. 200