So we're going to represent the problem: "If the numerator of a fraction is increased by 3, the fraction becomes 3/4" in an equation.
Let "n" be the numerator and let "d" be the denominator.
Since the numerator is increased by 3, we could represent this as n+3.
The denominator "d", is not suffering any change in this statement.
So, we can write:
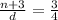
If we multiply by cross:

So, the answer is the first one.