Question

Monochromatic light passes through two narrow slits 0.23 mm apart and forms an interference pattern on a screen 1.67 m away. If light of wavelength 671.37 nm is used, what is the distance from the center of the central maximum to the center of the third order bright fringe in centimeters?

Answer 1

Given:

• Distance between slits = 0.23 mm

,

• Distance, d = 1.67 m

,

• Wavelength = 671.37 nm

Let's find the distance from the center of the central maximum to the center of the third order bright fringe.

To find the distance, apply the formula:

`y_m=(m\lambda L)/(d)`

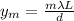
Where:

m = Third order = 3

λ is the wavelength = 67137 ncm

L = 1.67 m = 167 cm

d = 0.23 mm = 0.023 cm

Thus, we have:

`\begin{gathered} y_3=(3*67137*10^(-9)*10^*167)/(0.023) \\ \\ y_3=(0.033635)/(0.23) \\ \\ y_3=1.46\text{ cm} \end{gathered}`

Therefore, the distance is 1.46 centimeters.

ANSWER:

1.46 cm