Question

Not sure if I got the right answer and what to make sure I did it correctly. I got that the limit doesn't exist.

Answer 1

We know that the limit

`\lim_(x\to a)f(x)`

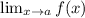
exists if and only if:

`\lim_(x\to a^-)f(x)=\lim_(x\to a^+)f(x)`

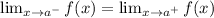
Let's calculate the left sided limit, for this limit we will use the first expression:

`\lim_(x\to8^-)f(x)=\lim_(x\to8^-)(x+10)=18`

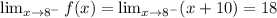
Let's find the right sided limit, for this limit we will use the second expression:

`\lim_(x\to8^+)f(x)=\lim_(x\to8^+)(10-x)=2`

We notice that these limits are not equal which means that the limit does not exist.

We can visualize this with the graph of the function which is shown below:

From the graph we notice that as we approach eight the value of the function is not the same for each side which means that the limit does not exist.